El mundo de los vectores
0. Introducción

Los invito a explorar cada uno de los contenidos de esta página, para afianzar sus conocimientos sobre "El mundo Vectorial"
Los invito a explorar cada uno de los contenidos de esta página, para afianzar sus conocimientos sobre "El mundo de los vectores".

1) ¿Crees que los vectores son importantes para el estudio de la física y de las situaciones cotidianas?¿Por qué?
2) ¿Qué opinas de la estrategia de aprender a sumar vectores de forma manipulable, así como lo hicimos enclase?
3) Has algún aporte o sugerencia que creas conveniente, o puedes preguntar sobre alguna duda que tengas del taller práctico.
1. La importancia de los vectores
Los vectores son muy importantes para estudiar fenómenos que suceden a nuestro alrededor. Con ellos podemos explicar por ejemplo: ¿Por qué si elevamos una comenta cuando el viento está soplando en contra, y empezamos a correr para mantenerla en el aire, ésta retrocede al punto en que la cuerda con la que la sostenemos, queda inclinada hacia atrás?
¿Por qué es importante de estudiar los vectores?
Los vectores son muy importantes para estudiar fenómenos que suceden a nuestro alrededor. Con ellos podemos explicar por ejemplo: ¿Por qué si elevamos una comenta cuando el viento está soplando en contra, y empezamos a correr para mantenerla en el aire, ésta retrocede al punto en que la cuerda con la que la sostenemos, queda inclinada hacia atrás?:
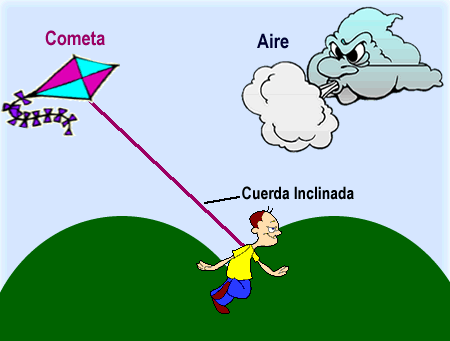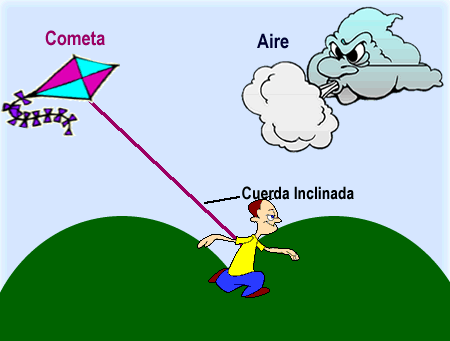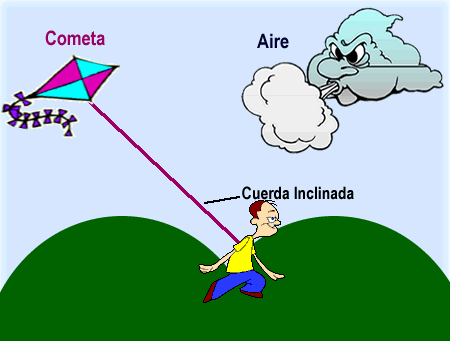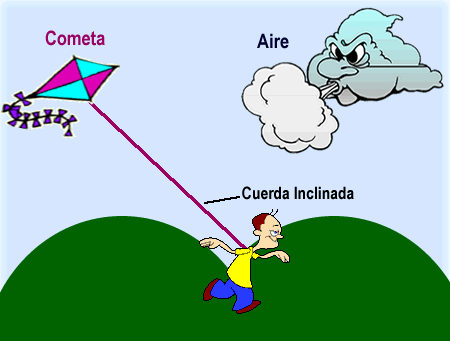
Para casos como este. Usamos los vectores para representar la velocidad que lleva la cometa y la velocidad del viento. Lo importante es ubicar los vectores en la dirección en la que se mueve cada uno, así:

Resulta que una de las tres características de los vectores, es que estos pooseen magnitud. Es decir, cada uno representa un valor numérico que para este caso, corresponde a la cantidad de velocidad que tiene el viento y la cometa.
Si ves de nuevo los vectores de arriba, notarás que uno es más largo que el otro. ¿Cierto?
Esto se debe a que para el ejemplo, el viento tiene más velocidad que la cometa y por eso su vector es más estirado. Por esta razón, es que la cometa se va hacia atrás de ti cuando corres con ella.
Lo que sucede es que al sumar gráficamente ambos vectores, el resultado es un vector que se dirige hacia atrás (más adelante te explicaremos cómo se deben ubicar los vectores para poder sumarlos gráficamente):
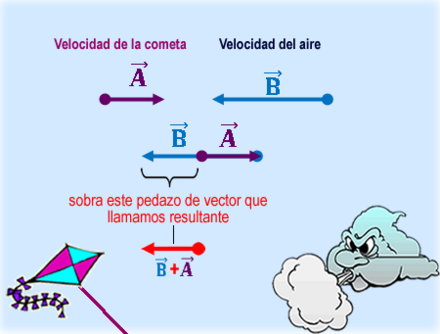
Este sería el vector que nos permite explicar por qué la cometa se va hacia atrás y no hacia adelante o por qué no se queda fija cuando la elevas contra el viento.
Conclusión:

Podemos decir que al hacer uso de los vectores (flechas dirigidas que poseen magnitud), podemos explicar mucho más fácil, problemas que tienen que ver con velocidades, desplazamientos, fuerzas y aceleraciones.
Estos son en realidad, fundamentales para el estudio de la física
2. Todo sobre vectores
Para poder estudiar a cerca de los vectores, es necesario identificar ¿Cuándo se usan?. Oberva el mapa y notarás que estos sólo los empleamos cuando estamos estudiando Magnitudes Vectoriales , porque es cuando necesitamos saber además de una magnitud (como 30 km/h), de una dirección (ángulo) y un sentido (Norte, sur, este, oeste). Justamente los vectores los podemos construir largos o cortos para representar la magnitud, los podemos graduar para indicar el ángulo y también los podemos orientar hacia el norte, el sur, el este o el oeste.
Esto nos permite entonces asegurar que para las magnitudes escalares no necesitamos vectores. Estas sólo se define con una magnitud (ejemplo: 3 segundos., no necesitamos decir 3 segundos al norte. Con sólo decir el tiempo y su cantidad numérica es suficiente).
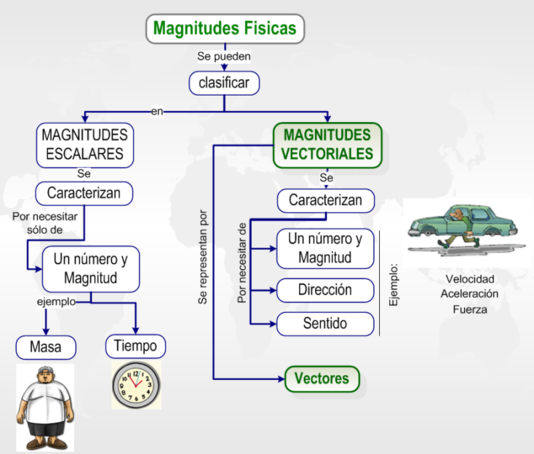
2.1 ¿Qué es un vector?
Un vector, es una flecha dirigida ( inclinada una cantidad de grados y orientanda hacia el Norte, Sur, Este, Oeste) que posee un valor numérico y una unidad de medida.
Por ejemplo:
Si queremos representar la velocidad de un caballo que se mueve a 30km/h hacia el Este.
Podemos hacer el vector que tenga: valor numérico 30, unidad de medida km/h, dirección 0º y sentido hacia el Este.
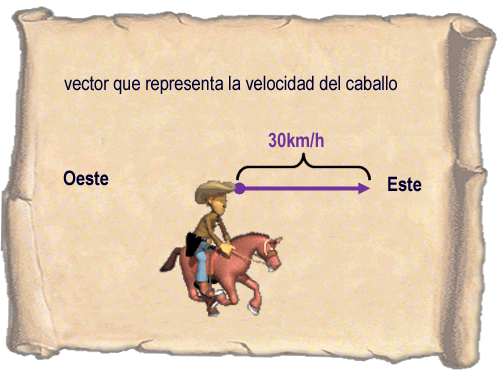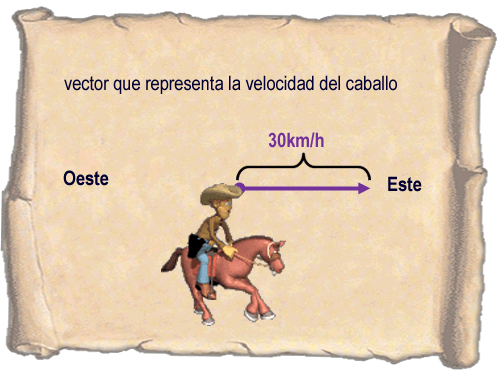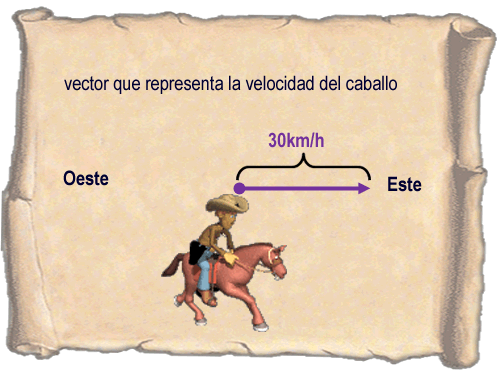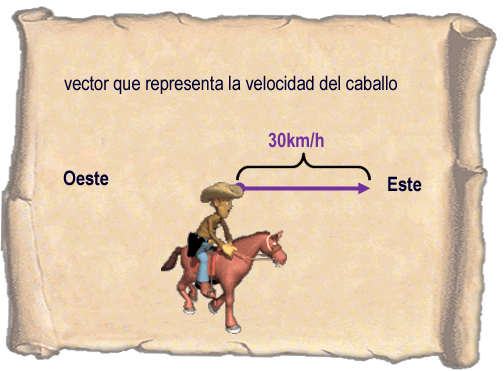
2.2 ¿Cómo simboliza un vector?
Los vectores los podemos simbolizar de dos formas:
1) Mediante una letra que puede ser mayúscula o minúscula y una flecha encima de ella.
2) Otra manera de simbolizar es poner en negrilla la letra
Si este fuera nuestro vector:


lo podríamos simbolizar como se muestra a la derecha:
y nos indicaría por ejemplo la velocidad de una bicicleta

2.3 Partes de un vector

Ya vimos que un vector se dibuja como una flecha dirigida. Ahora, es importante reconocer que esa flecha se compone de tres partes:
1) Una cola, también llamada punto inicial
2) Una cabeza, también conocida como punto final
3) Una longitud. Ten en cuenta que si tienes dos vectores y uno de ellos es más largo que el otro, es porque ese representa un vector con mayor magnitud.

2.4 Características
En la sección "Todo sobre Vectores", Te presentamos un mapa donde se identifica que los vectores son la forma como se representan las magnitudes vectoriales.

Ahora, es importante mencionar ¿Cuáles son sus 3 características fundamentales?:
1) MAGNITUD:
se refiere a ¿Cuanto mide el vector?.
Es el valor numérico acompañado de la unidad de medida, por ejemplo 8 N. El 8 es el número y N (se lee Newton) es la unidad de medida de la Fuerza.
¿Cómo simbolizamos la magnitud?
Recuerda que un vector se simboliza con una letra y una flecha arriba o con la letra en negrilla. Para referirnos a la magnitud o a la longitud del vector, usamos la letra con la flecha pero encerrada entre dos líneas o la letra sin negrilla, así:
2) DIRECCIÓN:
se refiere a ¿Qué tanto giro el vector?.
Es el que indica cuántos grados gira el vector

3) SENTIDO:
se refiere a ¿Hacia dónde dirijo el vector?
Es el que orienta el vector, puede ser hacia el norte, el sur, el este, el oeste, arriba, abajo, derecha o izquierda.

2.5 ¿Cómo sumo dos vectores?

Existen tres maneras de sumar vectores:
(Todas te las explicaremos más adelante)
2.6 ¿Cómo sumo más de dos vectores

Para que te sirva de ayuda en el desarrollo del taller. Te planteamos una situación en la que Homero muestra los vectores que indican su desplazamiento por las calles de Springfield, desde la Farmacia hasta el Hospital.
Para saber cuál es el desplazamiento final de la farmacia al hospital, lo que hacemos es empezar a sumar los vectores de dos en dos hasta llegar al vector final que termina en el hospital.
Veamos el proceso gráfico:
- Asignamos una letra que simbolice cada vector, para este caso usamos las letras en negrilla

- Ahora, tomamos los dos primeros vectores, es decir A y B y los sumamos gráficamente teniendo en cuenta las reglas de la suma:

- Bueno ya tenemos el primer vector suma. El siguiente paso para poder hallar el vector final que une la farmacia con el hospital, es tomar ese vector que resultó al sumar A con B y sumarlo con C, así:

- Ahora sumamos estos dos vectores y obtenemos el segundo vector suma:

- Si observas el dibujo, el segundo vector suma es el que resulta de sumar el vector A+B con el vector C.
- Continuamos ahora usando ese vector que resultó (A+B+C) y lo sumamos con D:

al sumar ambos vectores, obtenemos finalmente a:

- Si observas detenidamente, notarás que este último vector suma es el que une la farmacia con el hospital en línea recta.

Conclusión
Podemos sumar más de dos vectores, pero para hacerlo existen varios métodos. El más fácil y cómo, es el de sumar los dos primeros vectores para luego usar la resultante y sumarlo con el otro vector hasta llegar al vector final, así como se hizo para indicar el desplazamiento que Homero hace desde la Farmacia hasta el Hospital.
Esto te sirve como modelo para desarrollar el taller práctico.
3. Videos
Si tienes alguna duda sobre la manera como debes sumar los vectores para hallar la resultante del desplazamiento del parque a tu casa. puedes ver este video.
En él, te enterarás de una manera de sumar fácilmente todos los vectores que construiste











